State Machine and Synchronization

This is the second of two notes of Lamport's Time-Clock paper^[1]. The first one is here.

The problem

We will be focusing on how to use Logical Clock to solve an actual problem. The problem is to grant the resource to a process, that

1. a process which has been granted the resource must release it before it's granted to another process (mutex)
2. different requests for the resource must be granted in the other in which they are made **
3. if every process which is granted the resource eventually releases it, then every request is eventually granted

A centralized solution

The requirement(2) is non-trivial to satisfy. The most naive solution would be having a centralized master that assigns the resource to processes upon receiving the request. But it doesn't actually satisfy (2). Let's say P0 made two requests, R0 to the master and R1 to P1. P1 after receiving R1, made R2 to the master requesting for the resource. R2 can be received before R0. If the master naively assigns the resource upon receiving a request, (2) will be violated.

This can be solved with Logical Clock, which gives a partial ordering of all events. We can define a global ordering of all events that's consistent with the partial ordering by breaking ties in a deterministic way (e.g. t:Pi < t:Pj iff i < j). We can modify the previous naive algorithm a bit. Now each process not only needs to request resource from the master, it also keeps sending heartbeats to the master. Let's say t0:p0 is the first request. t0 will be the smallest request timestamp received by the master. Once the master has received messages, including heartbeats from all processes that have timestamp greater than t0, it can safely grant the resource to P0. The master will then wait until P0 releases the resource and then repeat the process. The master doesn't need to store all the heartbeat messages from all processes. It only needs to track the high watermark from every process and if the resource is currently available or not.

This works. But it has a few downsides.

• it's a centralized algorithm
• sending heartbeats can take a significant portion of the network bandwidth comparing to the actual request and release commands

A distributed solution

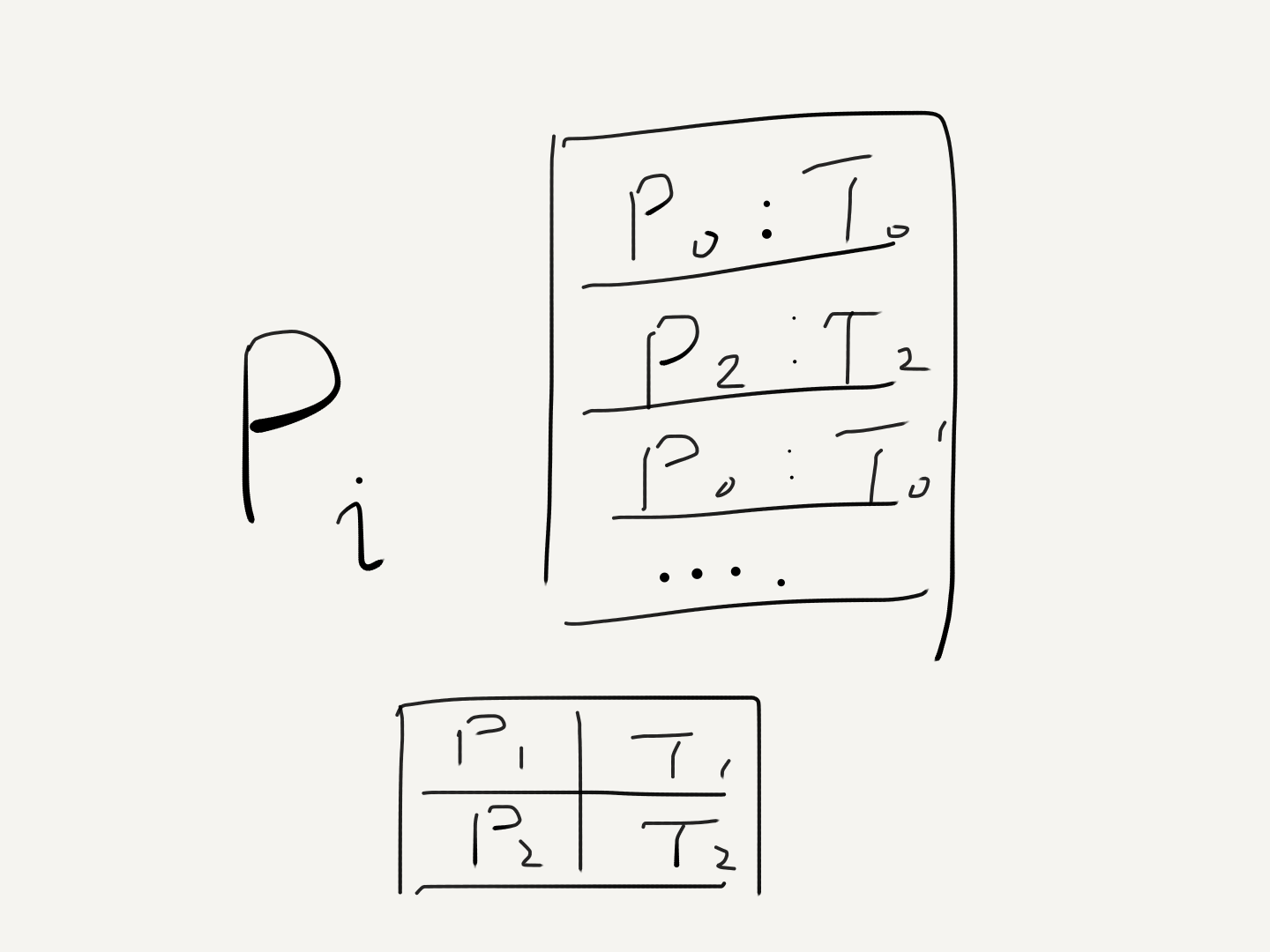
1. Every process sends request resource (timestamped) to everyone, and stores the request locally.
2. Upon receiving the request, each process stores the request and sends an ACK (timestamped) to the sender.
3. The resource is granted to a process Pi, when (i) req:Pi:Ti is in the local store and Ti is the smallest timestamp for a resource request locally (ii) Pi has received messages from all other processes with T > Ti
4. To release the resource, Pi sends release resource (timestamped) to everyone, and removes any req:Pi locally stored.
5. Upon receiving the release, each process also removes any req:Pi from the local store.

(There are a few assumptions made to make describing the algorithm simpler. E.g. messages are sent and received in order.)

It's pretty obvious that it satisfies all three requirements.

State Machine

If we generalize the solution above a little bit, it's not hard to see that it's actually a generic method for achieving synchronization in distributed system (without failures).

You can imagine that each process simply broadcasts timestamped commands to everyone. And everyone sends back ACK. Each process only executes a command when it satisfies the (3) above. In this way, all processes will eventually execute all commands in exactly the same order. If we model each process as a state machine, they all start with the same initial state. Then they will go through exactly the same sequence of state transitions due to applying (or executing) the same sequence of commands. And eventually end up in exactly the same end state, which achieves synchronization. They all do that independently without any centralized coordination.

Lamport likes to reason about things (either distributed system or a program) using state machine. It's used in the Paxos, and now in TLA+. They both originated from the state machine idea in this paper, the same old, Time-Clock paper.