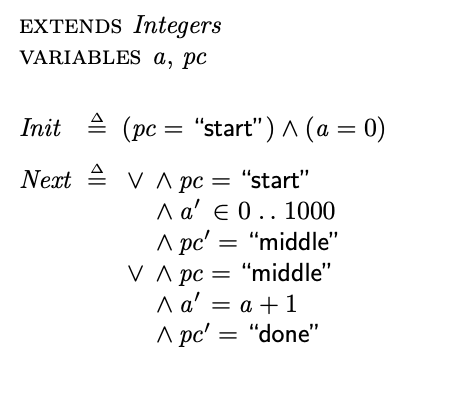Previous post can be found here – https://blog.the-pans.com/state-machine/. The entire series is based on Lamport's TLA+ tutorial.
In the previous post, we talked about any system can be described as a state machine. What language should we use to describe state machines? TLA+ uses mathematics, which is precise and forces the users to reason about systems abstractly.
Describing state machines using math
Let's describe this program (from the previous example), in math. This is what the original program looks like.
a = get_random_number(0, 1000)
a += 1This is how the state machine looks like described in code (pc stands for program counter).
if pc == start:
a = get_random_number(0, 1000)
else if pc == middle:
a += 1
else:
haltThis is how the state machine looks like described in math.
(pc = "start") ∧ (a' ∈ {0, .., 1000}) ∧ (pc' = "middle")
∨
(pc = "middle") ∧ (a' = a + 1) ∧ (pc' = "done")
This is not code. = is not assignment but equality instead. We're writing a formula relating a, pc, a', and pc'. The formula evaluates to either true or false based on the value of a, pc, a', and pc'.
For example, for a given state – a = 1, a' = 4, pc = "middel", pc' = "done", the formula would be evaluated to false because a' != a + 1 .
TLA+ supports the following syntactic sugar to make things look more like a bullet list.
∨ ∧ (pc = "start")
∧ (a' ∈ RANDOM_NUMBER_SET)
∧ (pc' = "middle")
∨ ∧ (pc = "middle")
∧ (a' = a + 1)
∧ (pc' = "done")
A complete spec
Usually a state machine has two parts – an initial state, and a state transition formula. Here's the complete TLA+ spec for the previous example.
EXTENDS Integers
VARIABLES a, pc
Init == (pc = "start") /\ (a = 0)
Next == \/ /\ pc = "start"
/\ a' \in 0..1000
/\ pc' = "middle"
\/ /\ pc = "middle"
/\ a' = a + 1
/\ pc' = "done"
The pretty printed version looks like the following.